skip-gram
具体过程与介绍见 cs224n 系列
从 one-hot 到 lookup-table
每一个单词经过 one-hot 编码后都会得到一个 $(V,1)$ 维的词向量, $V$ 个词就是 $(V,V)$ 维方阵。这样的话,矩阵的计算量会极大,所以要降维以减小计算量。
单词在 one-hot 编码表的位置是由关系的,如果单词出现的位置column = 3,那么对应的就会选中权重矩阵的Index = 3。由此可以通过这个映射关系进行以下操作:将one-hot编码后的词向量,通过一个神经网络的隐藏层,映射到一个低纬度的空间,并且没有任何激活函数。最后得到的东西就叫做 lookup-table,或叫 word embedding 词嵌入,维度 $(V,d)$。
数学原理
一个单词的极大似然估计概率计算公式在取负号后变为:
$$ J(\theta)=-\frac{1}{T}\sum^T_{t=1}\sum_{\substack{-m \le j \le m \\ j\neq0}}logP(w_{t+j} \ | \ w_t; \ \theta) $$代入softmax计算公式后得到目标函数或叫损失函数:
$$ logP(w_o \ | \ w_c)=u_o^Tv_c-log \Bigg( \sum_{i \in V}exp(u_i^Tv_c) \Bigg) $$用梯度下降更新参数:
$$ \frac{\partial logP(w_o \ | \ w_c)}{\partial v_c} = u_o-\sum_{j \in V}P(w_j \ | \ w_c)u_j $$训练结束后,对于词典中的任一索引为 $i$ 的词,我们均得到该词作为中心词和背景词的两组词向量 $vi$ , $u_i$ .
这里存在几个问题:
- 一个是在词典中所有的词都有机会被当做是“中心词”和“背景词”,那么在更新的时候,都会被更新一遍,这种时候该怎么确定一个词的向量到底该怎么选择呢?
- 在进行迭代的时候对系统消耗也是巨大的,因为每走一步就要对所有的单词进行一次矩阵运算。这种时候该如何进行优化呢?
- 负采样
- 层级softmax
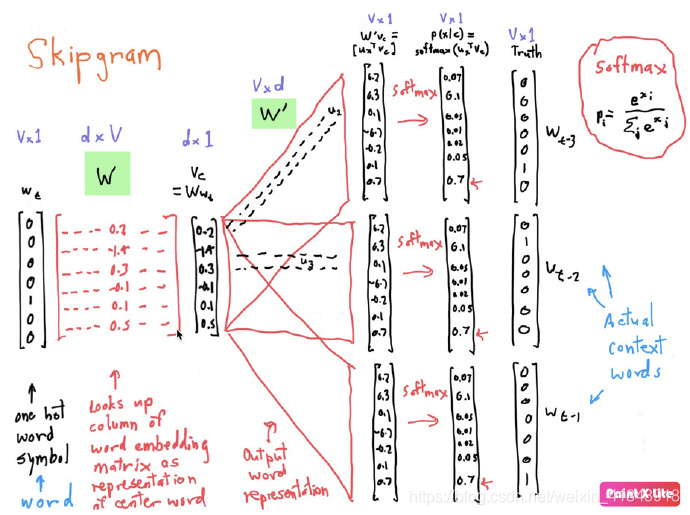
skip-gram 完整过程

skip-gram with negative sampling
负样本即非中心词的上下文,而使用梯度下降更新参数时会对所有的正负样本一起更新。为减少计算量,遂引入 negative sampling 负采样。
负采样在更新负样本的参数时只考虑其中的一小部分,且是随机选择一个负样本集合。此时,对上面公式的优化目标即最大正样本概率之外又添加了最小化负样本概率。
而 softmax 的计算量也很大,同时对于词嵌入的前身 one-hot 也能看出skip-gram的任务更偏向于二分类,所以可以使用 sigmoid $\sigma(x)=\frac{1}{1+exp(-x)}$ 来降低计算量。
可以得到以下新的目标函数:
$$ L=- \bigg[\sum log \ \sigma(c_{pos}·w)+\sum log \ \sigma(-c_{neg}·w) \bigg] $$其中 $w$ 表示目标词对应的词向量,$c$ 表示目标词的上下文对应的词向量。
训练方法则选用 Stochastic gradient descent 随机梯度下降 来完成参数的更新。
随机梯度下降法的思想就是按照数据生成分布抽取 $m$ 个样本,通过计算他们梯度的平均值来更新梯度,梯度下降法采用的是全部样本的梯度平均值来更新梯度。则目标函数又变为:
$$ L=- \bigg[log \ \sigma(c_{pos}·w)+\sum^k_{i=1} log \ \sigma(-c_{neg}·w) \bigg] $$使用链式法则计算梯度:
$$ \begin{align} \frac{\partial L}{\partial w}=&-\bigg[\frac{\partial}{\partial w}(log \ \sigma(c_{pos}·w))+\frac{\partial}{\partial w}(\sum^k_{i=1}log \ \sigma(-c_{neg_i}·w))\bigg] \\ =& [\sigma(c_{pos}·w)-1]c_{pos}+\sum^k_{i=1}[\sigma(c_{neg_i})·w]c_{neg_i} \end{align} $$则SGD阶段的参数更新为:
$$ w^{t+1}=w^t-\alpha \bigg \{[\sigma(c_{pos}·w)-1]c_{pos}+\sum^k_{i=1}[\sigma(c_{neg_i})·w]c_{neg_i} \bigg\} $$最后,通常会将两个词向量进行相加来表述单词。例如第 $i$ 个单词就可以表示为$ w_i+c_i$ 。