LSTM
长短期记忆(Long short-term memory, LSTM)是一种特殊的 RNN,主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的 RNN,LSTM 能够在更长的序列中有更好的表现。
门结构中的激活函数
门结构中包含着 sigmoid 激活函数。sigmoid 激活函数与 tanh 函数类似,不同之处在于 sigmoid 是把值压缩到 0~1 之间而不是 -1~1 之间。这样的设置有助于更新或忘记信息,因为任何数乘以 0 都得 0,这部分信息就会剔除掉。同样的,任何数乘以 1 都得到它本身,这部分信息就会完美地保存下来。这样网络就能了解哪些数据是需要遗忘,哪些数据是需要保存。这也代表着门结构最后计算得到的是一个概率。
遗忘门
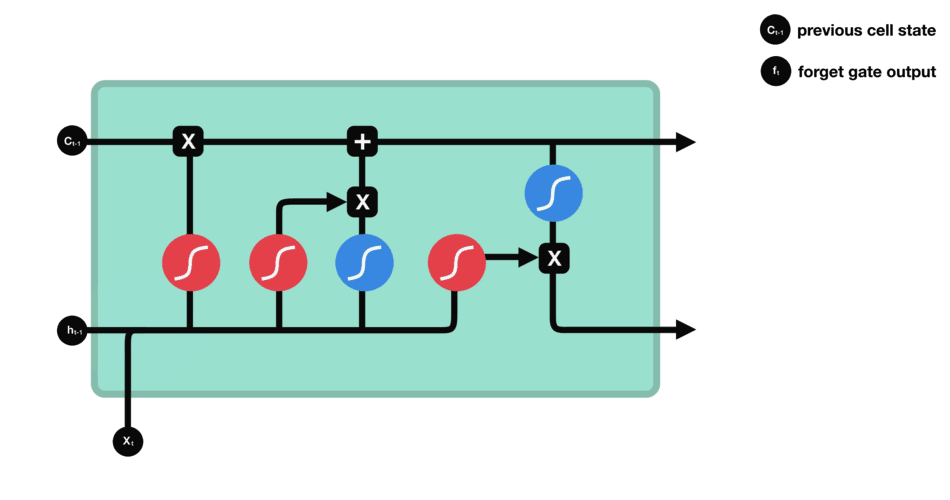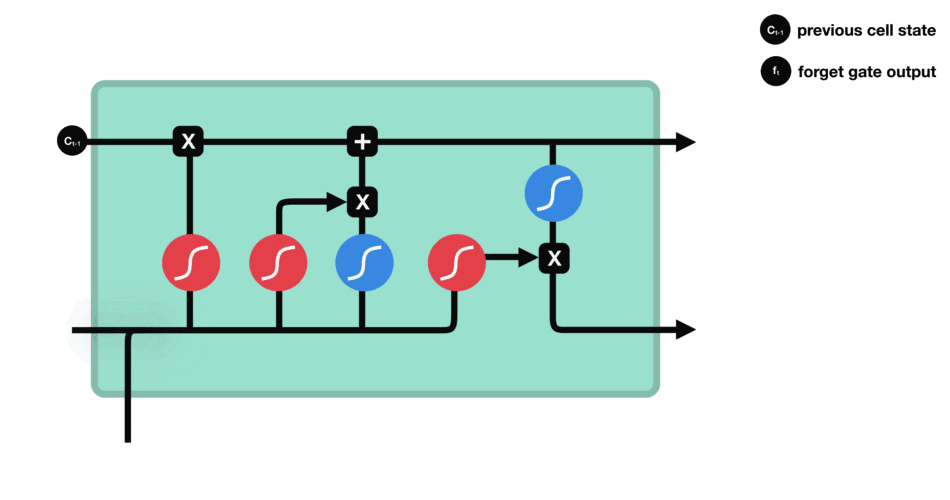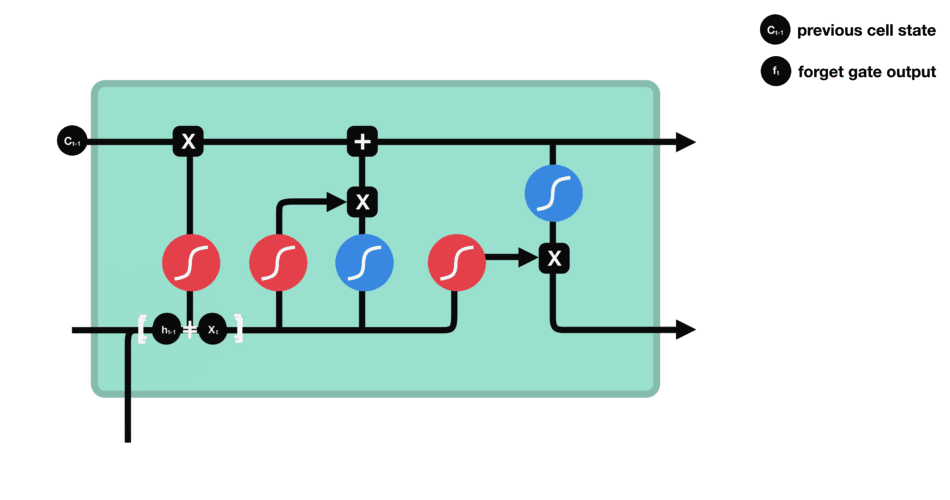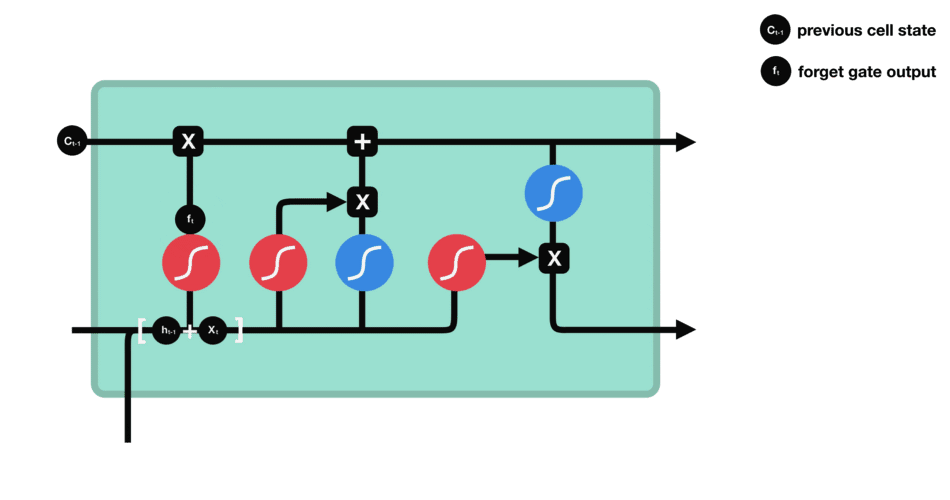
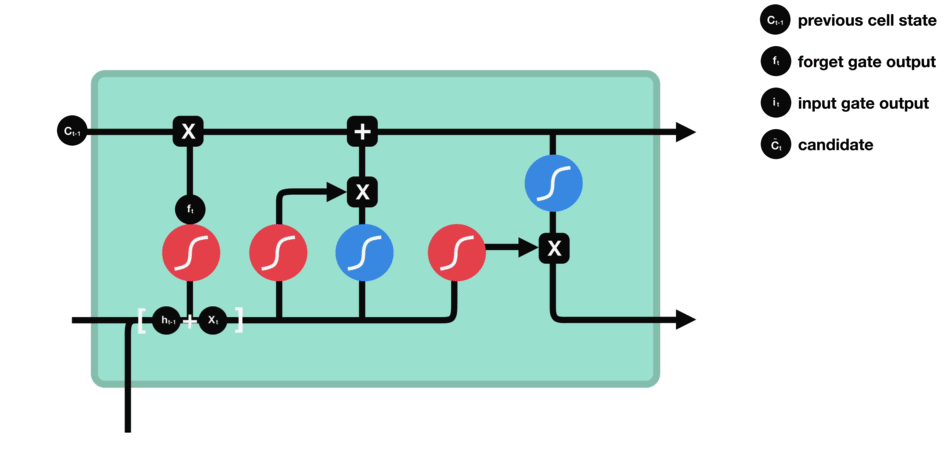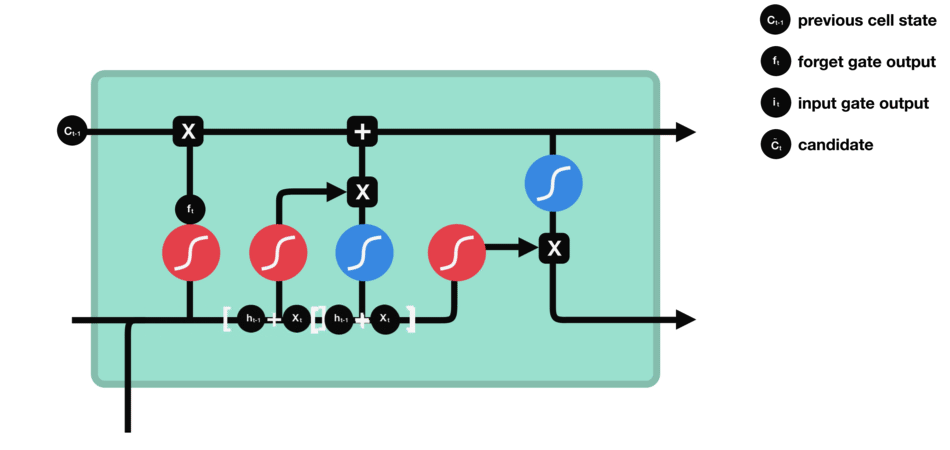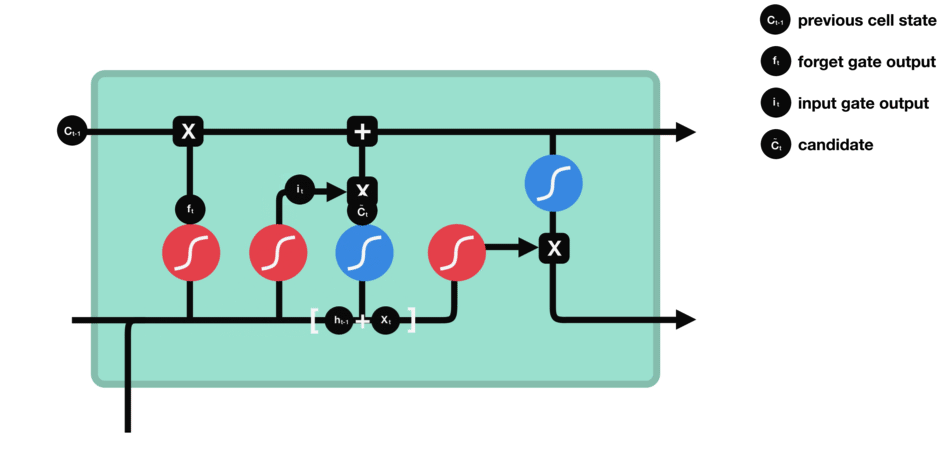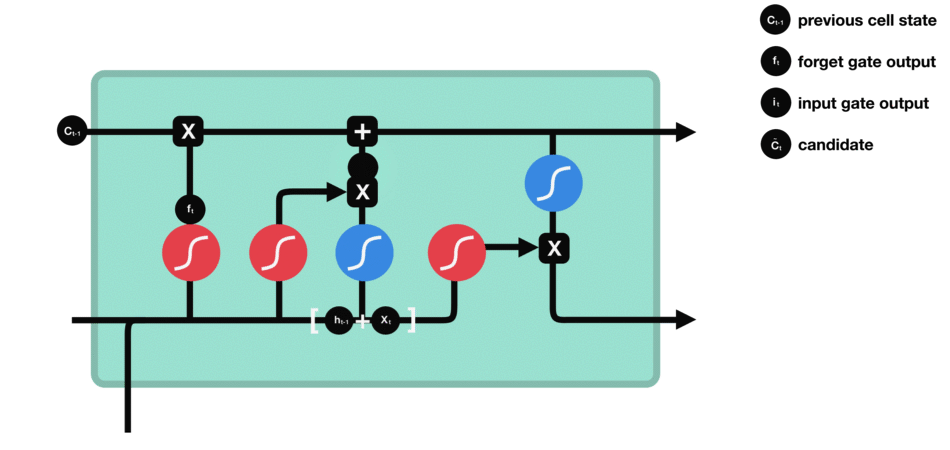
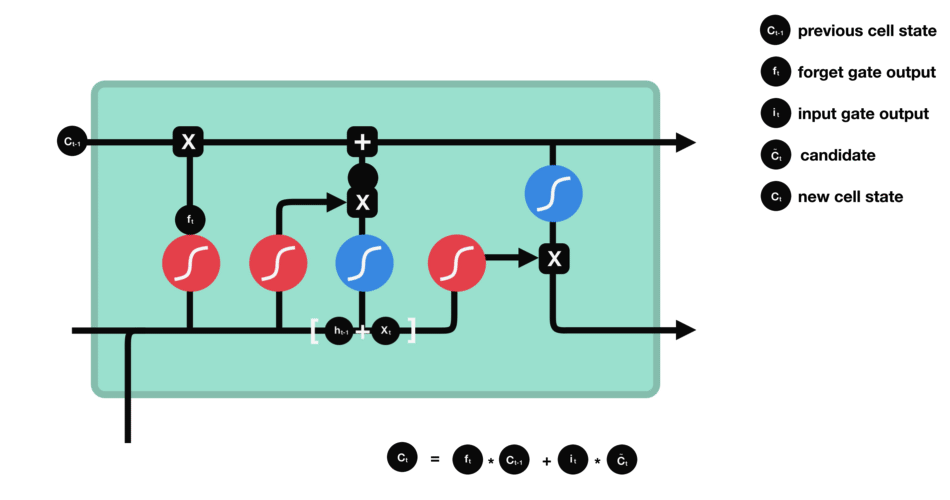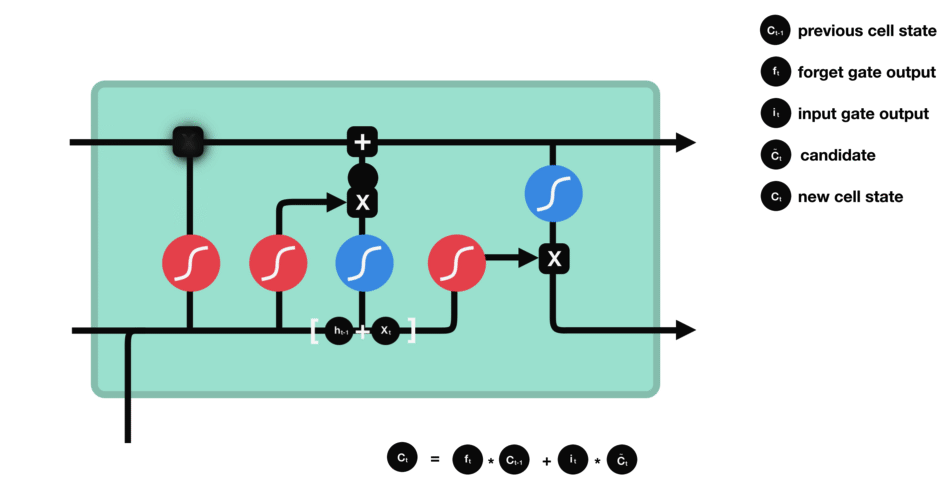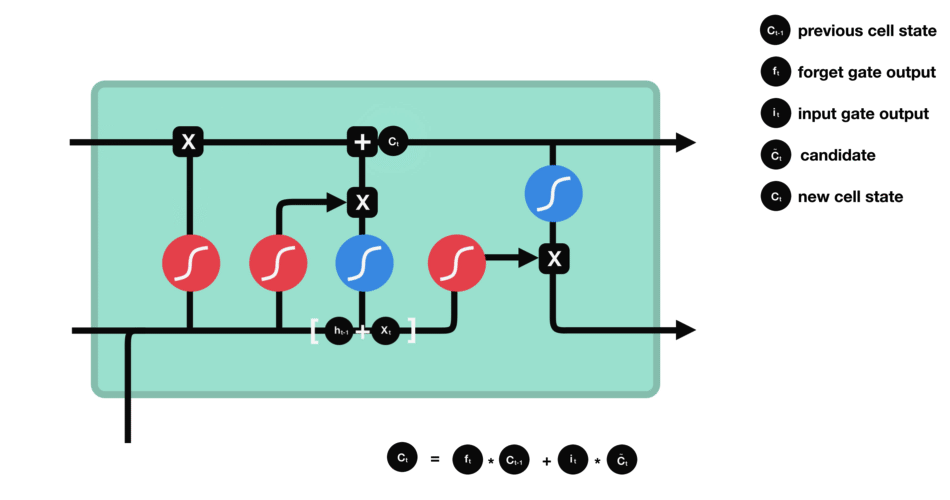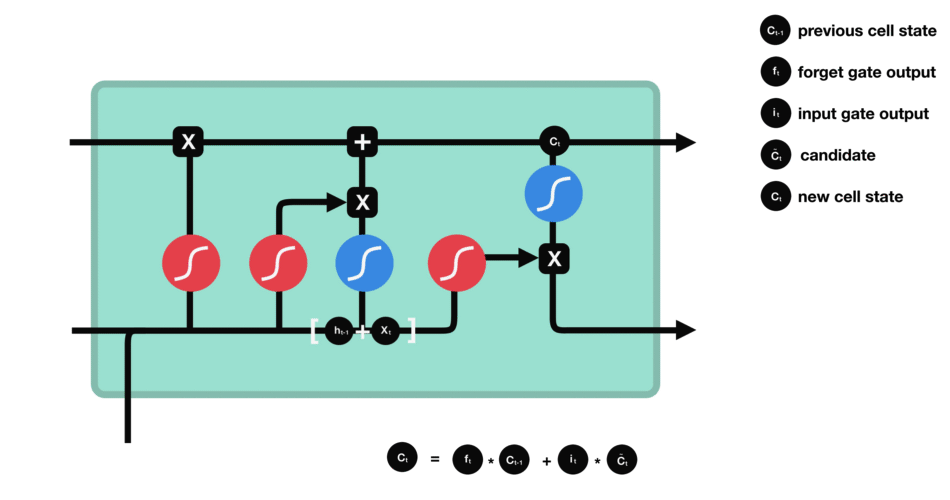
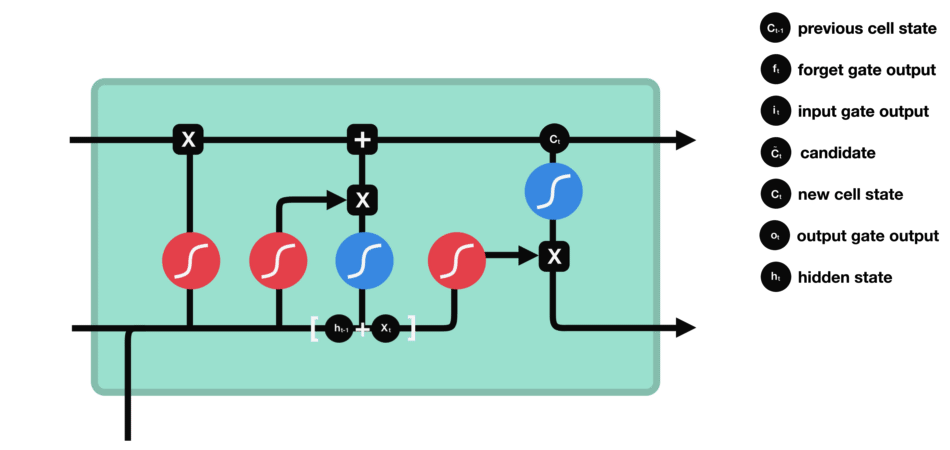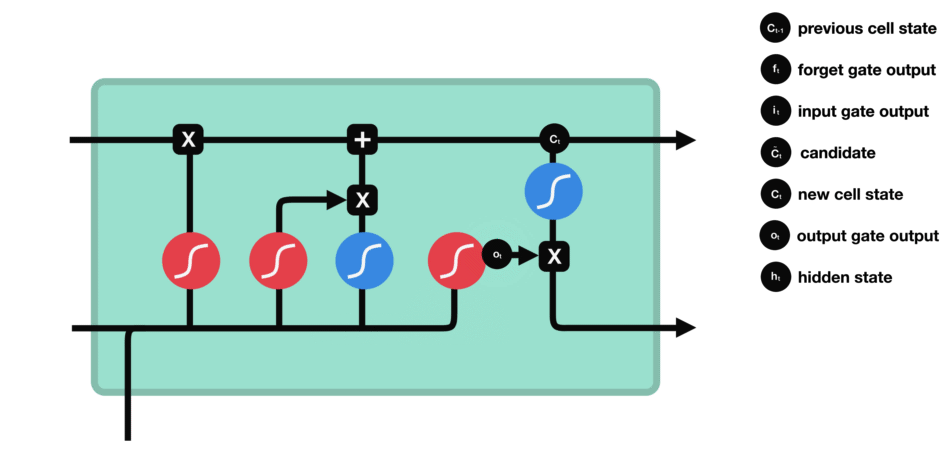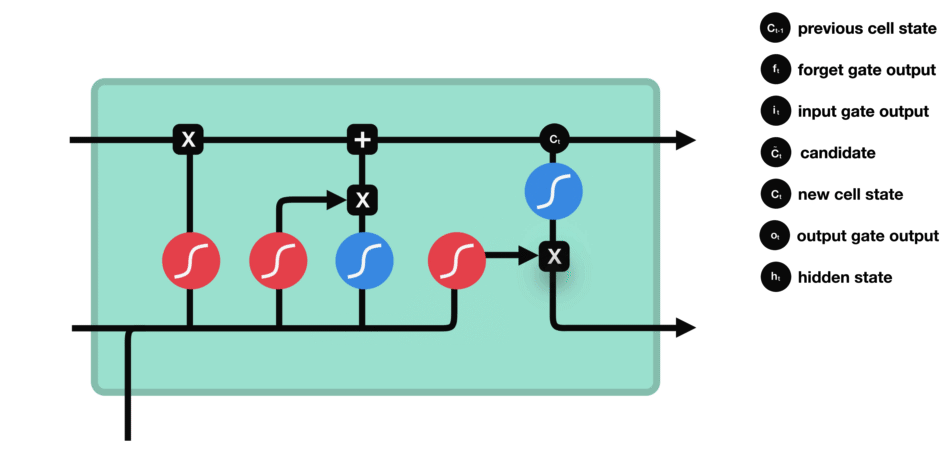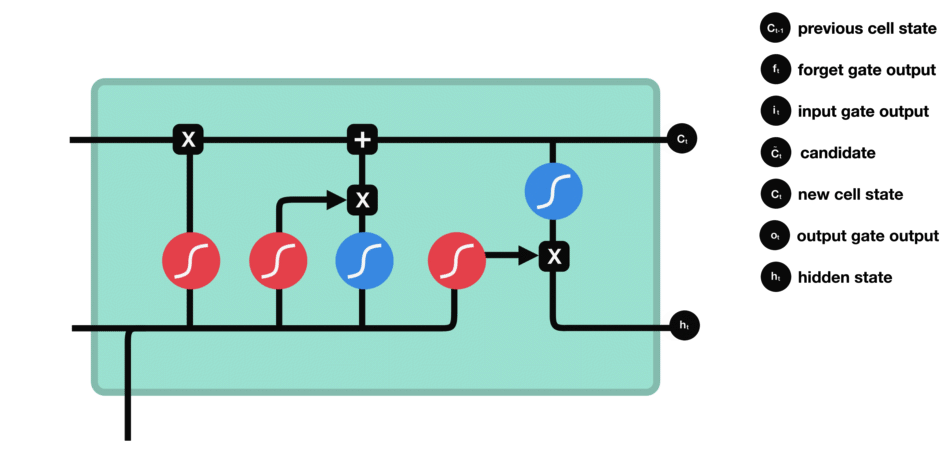
遗忘门的功能是决定应丢弃或保留哪些信息。来自前一个隐藏状态的信息和当前输入的信息同时传递到 sigmoid 函数中去,输出值介于 0 和 1 之间,越接近 0 意味着越应该丢弃,越接近 1 意味着越应该保留。
输入门
输入门用于更新细胞状态。首先将前一层隐藏状态的信息和当前输入的信息传递到 sigmoid 函数中去。将值调整到 0~1 之间来决定要更新哪些信息。0 表示不重要,1 表示重要。
细胞状态
下一步,就是计算细胞状态。首先前一层的细胞状态与遗忘向量逐点相乘。如果它乘以接近 0 的值,意味着在新的细胞状态中,这些信息是需要丢弃掉的。然后再将该值与输入门的输出值逐点相加,将神经网络发现的新信息更新到细胞状态中去。至此,就得到了更新后的细胞状态。
输出门
输出门用来确定下一个隐藏状态的值,隐藏状态包含了先前输入的信息。首先,我们将前一个隐藏状态和当前输入传递到 sigmoid 函数中,然后将新得到的细胞状态传递给 tanh 函数。
最后将 tanh 的输出与 sigmoid 的输出相乘,以确定隐藏状态应携带的信息。再将隐藏状态作为当前细胞的输出,把新的细胞状态和新的隐藏状态传递到下一个时间步长中去。
数学计算方式
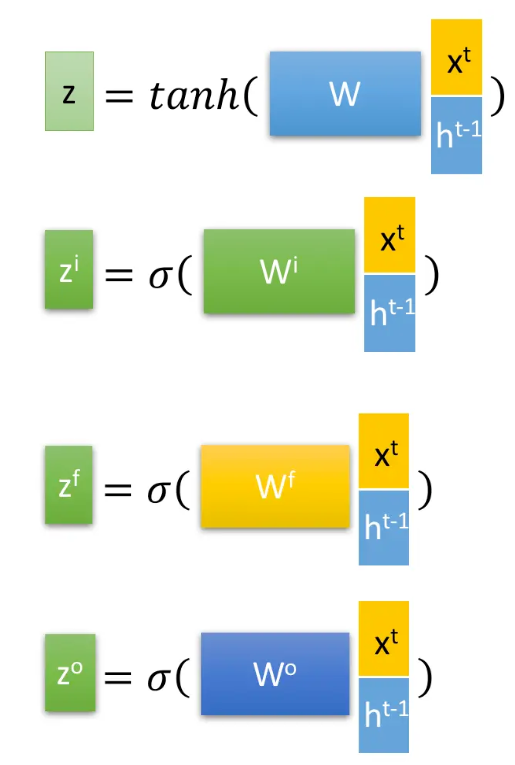
其中,$W$ 为当前层权重矩阵,$t$ 表示 timestep,$i,f,o$ 分别为输入门、遗忘门、输出门,第一个 $Z$ 为输出向量,$\sigma$ 为 sigmoid 。
总结
LSTM内部主要有三个阶段:
- 忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的,记住重要的”。通过计算得到的 $z^f$ 来作为忘记门控,来控制上一个状态的 $c^{t−1}$ 哪些需要留哪些需要忘。
- 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入 $x^t$ 进行选择记忆。当前的输入内容由前面计算得到的 $z$ 表示。而选择的门控信号则是由 $z^i$ 来进行控制。
- 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 $z^o$ 来进行控制的。
通过门控状态来控制传输状态,记住需要长时间记忆的,忘记不重要的信息;而不像普通的RNN那样只能够“呆萌”地仅有一种记忆叠加方式。对很多需要“长期记忆”的任务来说,尤其好用。
但也因为引入了很多内容,导致参数变多,也使得训练难度加大了很多。因此很多时候我们往往会使用效果和LSTM相当但参数更少的 GRU 来构建大训练量的模型。
GRU
GRU 与 LSTM 非常相似。与 LSTM 相比,GRU 去除掉了细胞状态,使用隐藏状态来进行信息的传递。它只包含两个门:更新门和重置门。
数学计算方式
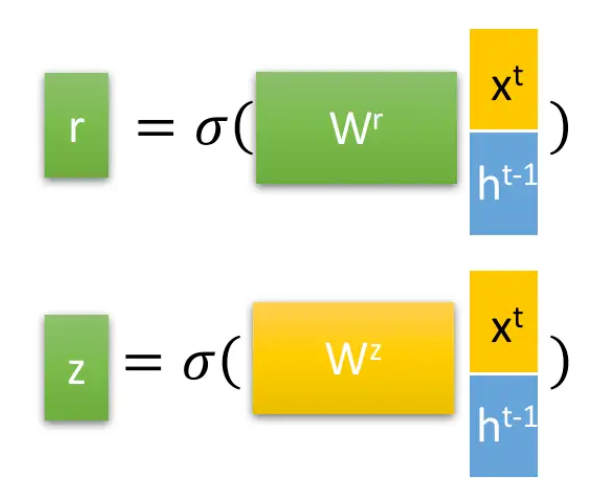
上面的 $r,z$ 分别为重置门、更新门。
重置门
得到门控信号之后,首先使用重置门控来得到**“重置”**之后的数据 $h^{t-1'}=h^{t-1} \odot r$ ,之后进行以下运算。
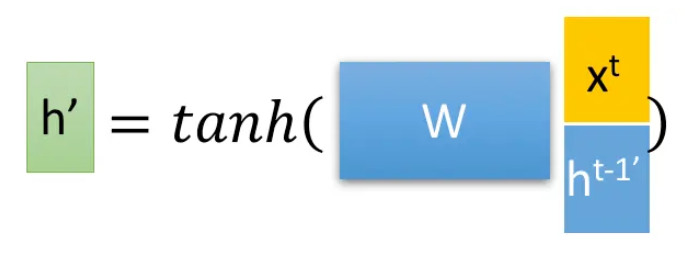
这里的 $h^′$ 主要是包含了当前输入的 $x^t$ 数据。有针对性地对 $h^′$ 添加到当前的隐藏状态,相当于”记忆了当前时刻的状态“,类似于LSTM的选择记忆阶段。
更新门
计算公式:
$$ h^t=(1-z) \odot h^{t-1} + z \odot h^{'} $$使用了同一个门控 $z$ 就同时可以进行遗忘和选择记忆。
公式中的前半部分表示对原本隐藏状态的选择性“遗忘”,后半部分表示对包含当前节点信息的 $h^{′}$ 进行选择性”记忆“。
总结
GRU输入输出的结构与普通的RNN相似,其中的内部思想与LSTM相似。
与LSTM相比,GRU内部少了一个”门控“,参数比LSTM少,但是却也能够达到与LSTM相当的功能。