Issues with recurrent models
Linear interaction distance
RNNs are unrolled “left-to-right”
Problem: RNNs take O(sequence length) steps for distant word pairs to interact
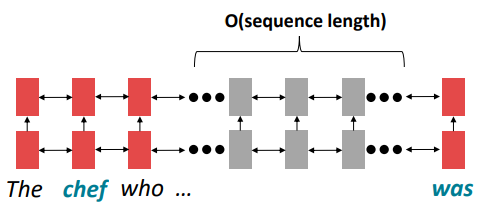
What does the O Problem means ?
- Hard to learn long-distance dependencies (because gradient problems! )
- Linear order of words is “baked in”; we already know linear order isn’t the right way to think about sentences…
Lack of parallelizability
- Forward and backward passes have O(sequence length) unparallelizable operations
- GPUs can perform a bunch of independent computations at once, but future RNN hidden states can’t be computed in full before past RNN hidden states have been computed
Self-Attention
Recall: Attention operates on queries, keys, and values.
- Each query $q_i$ , key $k_i$ and value $v_i$ has follows: $$ q_i \in \R^d, \ k_i \in \R^d, \ v_i \in \R^d $$
In self-attention, the queries, keys, and values are drawn from the same source.
- For example, if the output of the previous layer is $x_1, ..., x_T$ (one vec per word), we cloud let $v_i=k_i=q_i=x_i$ (that is, use the same vectors for all of them)
The (dot product) self-attention operation is as follows:
$$ e_{ij}=q_i^Tk_j \\ \alpha=\frac{exp(e_{ij})}{\sum_{j^{'}}exp(e_{ij^{'}})} \\ output_i=\sum_j\alpha_{ij}v_j $$Fixing the first self-attention problem: sequence order
Since self-attention doesn’t build in order information, we need to encode the order of the sentence in our keys, queries, and values.
Consider representing each sequence index as a vector :
$$ p_i \in \R^d, \ for \ i \in \{1,2,...,T\} \ are \ postion \ vectors $$Easy to incorporate this info into our self-attention block: just add the $p_i$ to our inputs.
Let $\hat{v},\hat{k},\hat{q}$ be our old values, keys, and queries.
$$ v_i = \hat{v_i}+p_i \\ q_i = \hat{q_i}+p_i \\ k_i = \hat{k_i}+p_i $$Position representation vectors through sinusoids
Sinusoidal position representations: concatenate sinusoidal functions of varying periods
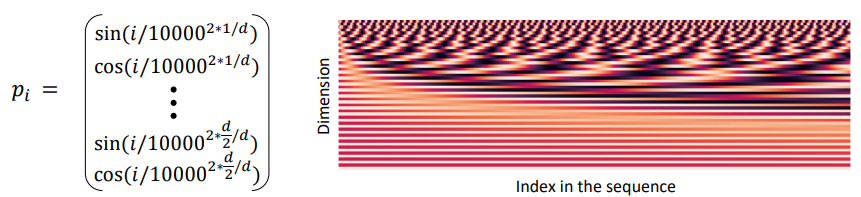
Pros:
- Periodicity indicates that maybe “absolute position” isn’t as important
- Maybe can extrapolate to longer sequences as periods restart
Cons:
- Not learnable; also the extrapolation doesn’t really work
Position representation vectors learned from scratch
Learned absolute position representations: Learn a matrix $p \in \R^{d \times T }$ , and let each $p_i$ be a column of that matrix.
Pros:
- Flexibility: each position gets to be learned to fit the data
Cons:
- Definitely can’t extrapolate to indices outside $1,...,T$
Fixing the second self-attention problem: Nonlinearities
Easy fix: add a feed-forward network to post-process each output vector
Fixing the third self-attention problem: Mask
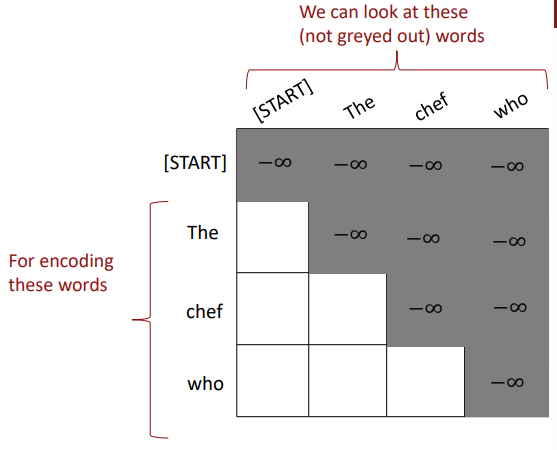
To use self-attention in decoders, we need to ensure we can’t peek at the future.
To enable parallelization, we mask out attention to future words by setting attention scores to $-\infty$
overall, necessities for a self-attention building block

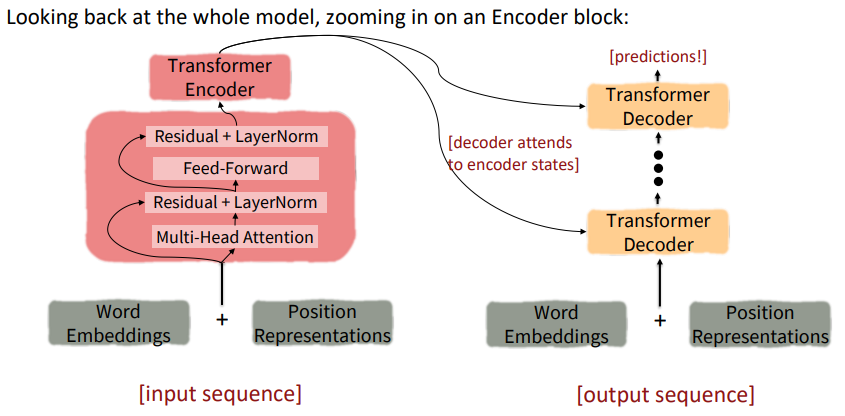
The Transformer Encoder
Key-Query-Value Attention

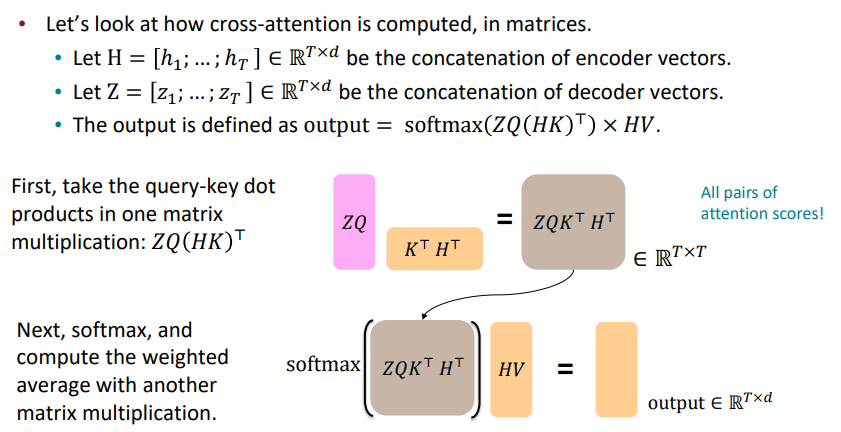
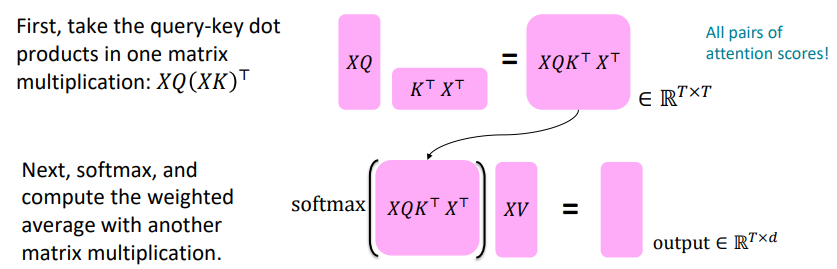
Let’s look at how key-query-value attention is computed, in matrices.
- Let $X=[x_1;...;x_T] \in \R^{T \times d}$ be the concatenation of input vectors
- First, note that $XK \in \R^{T \times d}, \ XQ \in \R^{T \times d}, \ XV \in \R^{T \times d}$
- The output is defined as $output=softmax(XQ(XK)^T)\times XV$
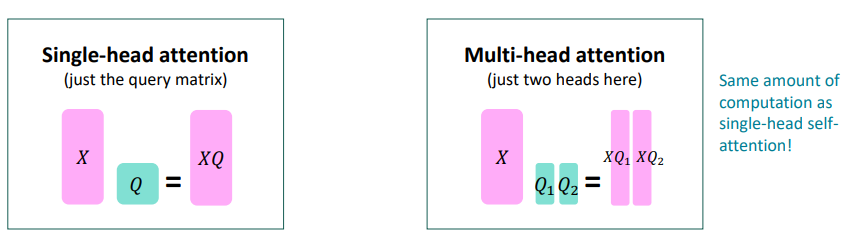
Multi-headed attention

Residual connections
见我的这篇文章 残差连接 | KurongBlog (705248010.github.io)
Layer normalization

Scaled Dot Product
“Scaled Dot Product” attention is a final variation to aid in Transformer training.
When dimensionality $𝑑$ becomes large, dot products between vectors tend to become large.
- Because of this, inputs to the softmax function can be large, making the gradients small
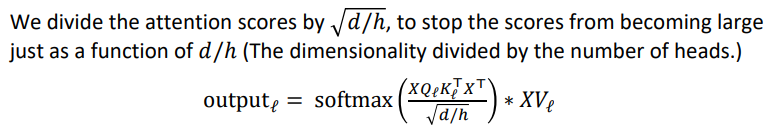
The Transformer Encoder-Decoder
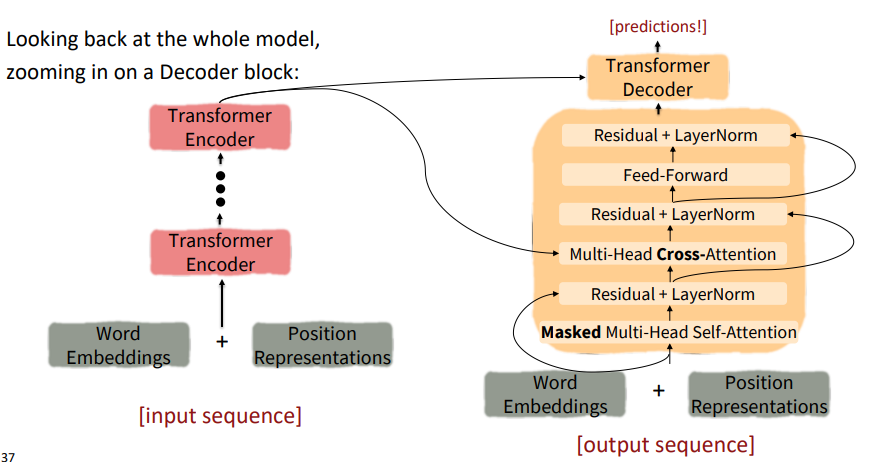
The Transformer Decoder
Cross-attention