Sequence-to-sequence with attention
Attention: in equations
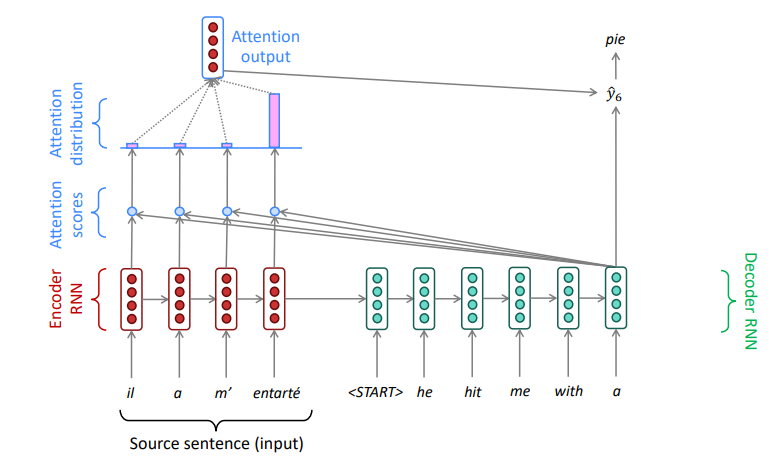
We have encoder hidden states $h_1,...,h_N \in \R^h$
On timestep $t$ , we have decoder hidden state $s_t \in \R^h$
We get the attention scores $e^t$ for this step:
$$ e^t=[s^T_th_1,...,s^T_th_N] \in \R^N $$We take softmax to get the attention distribution $\alpha^t$ for this step (this is a probability distribution and sums to 1)
$$ \alpha^t=softmax(e^t) \in \R^N $$We use $\alpha^t$ to take a weighted sum of the encoder hidden states to get the attention output $a_i$
$$ a_i=\sum^N_{i=1}\alpha_i^th_i \in \R^h $$Finally we concatenate the attention output $a_t$ with the decoder hidden state $s_t$ and proceed as in the non-attention seq2seq model
$$ [a_t;s_t] \in \R^{2h} $$
Attention is great
- Attention significantly improves NMT performance
- Attention provides more “human-like” model of the MT process
- Attention solves the bottleneck problem
- Attention helps with the vanishing gradient problem
- Provides shortcut to faraway states
- Attention provides some interpretability
- By inspecting attention distribution, we can see what the decoder was focusing on
There are several attention variants

Attention variants

Attention is a general Deep Learning technique
More general definition of attention:
- Given a set of vector values, and a vector query, attention is a technique to compute a weighted sum of the values, dependent on the query.
The weighted sum is a selective summary of the information contained in the values, where the query determines which values to focus on.
Attention is a way to obtain a fixed-size representation of an arbitrary set of representations (the values), dependent on some other representation (the query).