Basic Tricks on NN
L2 Regularization
A full loss function includes regularization over all parameters $\theta$ , e.g., L2 regularization:
$$ J(\theta)=f(x)+\lambda \sum_k \theta^2_k $$Regularization produces models that generalize well when we have a “big” model.
Dropout
- Training time: at each instance of evaluation (in online SGD-training), randomly set 50% of the inputs to each neuron to 0
- Test time: halve the model weights (now twice as many)
- This prevents feature co-adaptation
- Can be thought of as a form of model bagging (i.e., like an ensemble model)
- Nowadays usually thought of as strong, feature-dependent regularizer
Vectorization
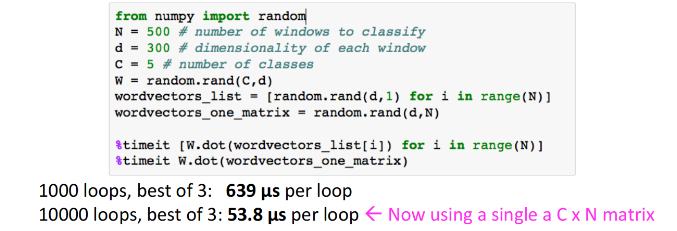
Always try to use vectors and matrices rather than for loops.
Non-linearities, old and new
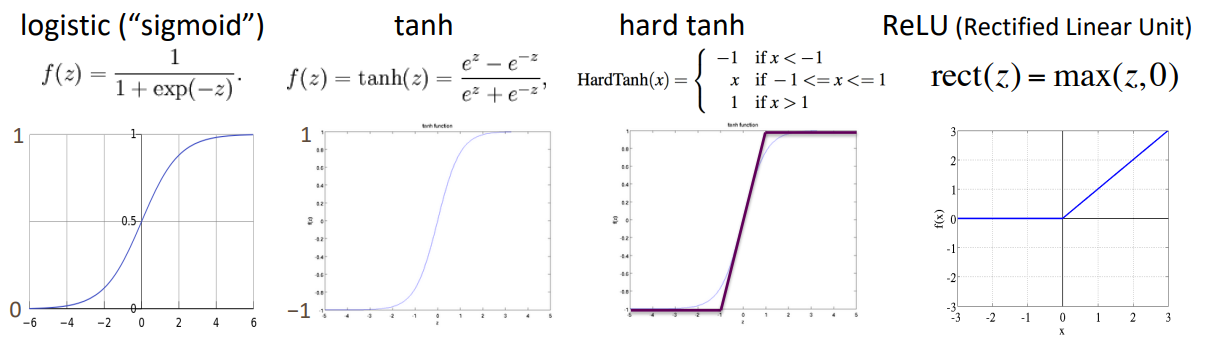
For building a deep network, the first thing you should try is ReLU — it trains quickly and performs well due to good gradient backflow.
Parameter Initialization
You normally must initialize weights to small random values. To avoid symmetries that prevent learning/specialization.
Initialize hidden layer biases to 0 and output (or reconstruction) biases to optimal value if weights were 0 (e.g., mean target or inverse sigmoid of mean target)
Initialize all other weights ~ Uniform($–r$, $r$), with $r$ chosen so numbers get neither too big or too small
Xavier initialization has variance inversely proportional to fan-in $n_{in}$ (previous layer size) and fan-out $n_{out}$ (next layer size):
$$ Var(W_i)=\frac{2}{n_{in}+n_{out}} $$
Optimizers
- Usually, plain SGD will work just fine
- These models give differential per-parameter learning rates
- Adagrad
- RMSprop
- Adam: A fairly good, safe place to begin in many cases
- SparseAdam
Learning Rates
- You can just use a constant learning rate. It must be order of magnitude right – try powers of 10
- Too big: model may diverge or not converge
- Too small: your model may not have trained by the assignment deadline
- By a formula: $lr=lr_0e^{-kt}$ , for epoch $t$
- There are fancier methods like cyclic learning rates
Language Modeling
Language Modeling is the task of predicting what word comes next. A system that does this is called a Language Model.
n-gram Language Models
A n-gram is a chunk of $n$ consecutive words.
- unigrams: “the”, “students”, “opened”, ”their”
- bigrams: “the students”, “students opened”, “opened their”
- trigrams: “the students opened”, “students opened their”
- 4-grams: “the students opened their”
We make a Markov assumption 马尔可夫假设: $x^{t+1}$ depends only on the preceding $n-1$ words
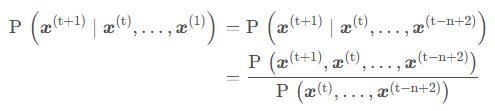
So we can get n-gram and (n-1)-gram probabilities by counting them in corpus of text.
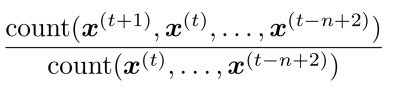
Example

Sparsity Problems with n-gram
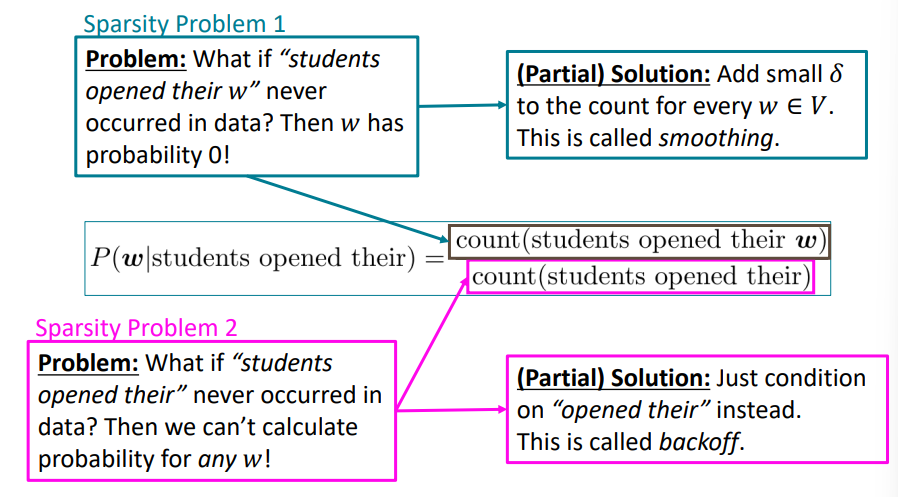
Note: Increasing n makes sparsity problems worse. Typically, we can’t have $n$ bigger than 5.
Storage Problems with n-gram

Recurrent Neural Networks (RNN)
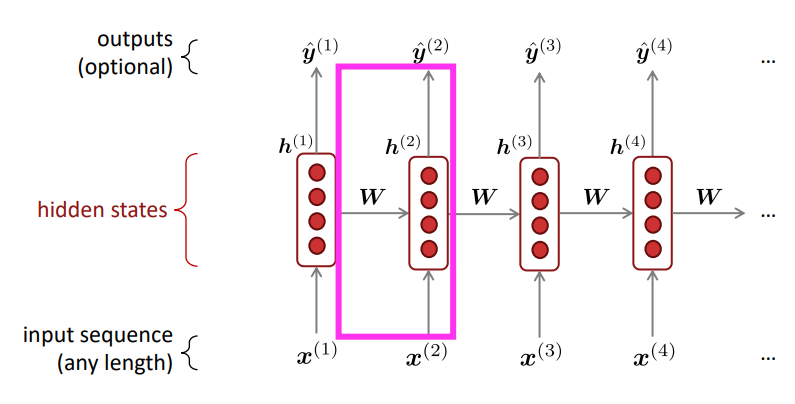
RNN Advantages:
- Can process any length input
- Computation for step $t$ can (in theory) use information from many steps back
- Model size doesn’t increase for longer input context
- Same weights applied on every timestep, so there is symmetry in how inputs are processed
RNN Disadvantages:
- Recurrent computation is slow
- In practice, difficult to access information from many steps back
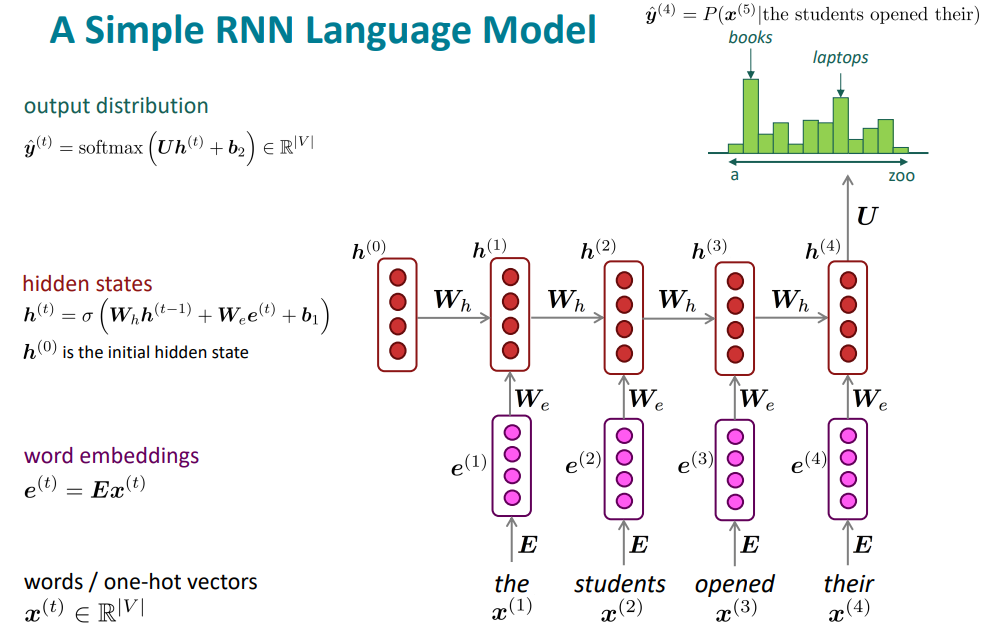
A Simple RNN Language Model