Meaning
Definition: meaning 语义
- the idea that is represented by a word, phrase, etc.
- the idea that a person wants to express by using words, signs, etc.
- the idea that is expressed in a work of writing, art, etc.
WordNet
Common NLP solution: Use, e.g., WordNet, a thesaurus containing lists of synonym (同义词) sets and hypernyms (上位词) (“is a” relationships).
Problems with resources like WordNet
Great as a resource but missing nuance
Missing new meanings of words
Subjective
Requires human labor to create and adapt
Can’t compute accurate word similarity
Representing words as discrete symbols

Word Vectors
Distributional semantics 分布式语义: A word’s meaning is given by the words that frequently appear close-by.
- When a word $w$ appears in a text, its context 上下文 is the set of words that appear nearby (within a fixed-size window).
- Use the many contexts of $w$ to build up a representation of $w$
word vectors are also called word embeddings 词嵌入 or (neural) word representations.
Word2vec
Word2vec (Mikolov et al. 2013) is a framework for learning word vectors.
- Every word in a fixed vocabulary is represented by a vector
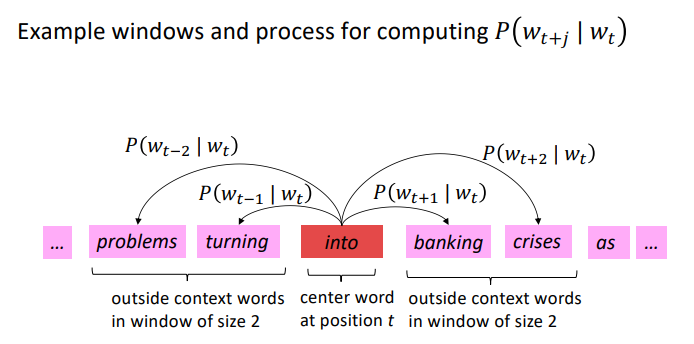
- Go through each position $t$ in the text, which has a center word $c$ and context (“outside”) words $o$
- Use the similarity of the word vectors for $c$ and o to calculate the probability of $o$ given $c$
- Keep adjusting the word vectors to maximize this probability
For Word2vec, its objective function $J(\theta)$ is the negative log likelihood:
$$ J(\theta)=-\frac{1}{T}\sum^T_{t=1}\sum_{\substack{-m \le j \le m \\ j\neq0}}logP(w_{t+j} \ | \ w_t; \ \theta) $$As the function, maximizing predictive accuracy transfers to minimizing objective function.
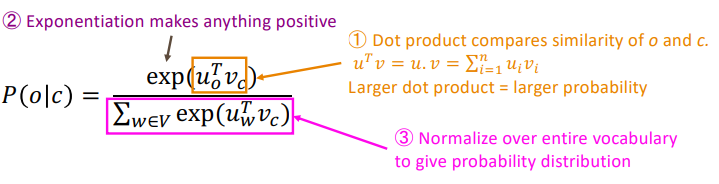
We use $v_w$ when $w$ is a center word and $u_w$ when $w$ is a context word. We will use two vectors, a center word $c$ and a context word $o$ :
$$ P(o|c) = \frac{exp(u^T_ov_c)}{\sum_{w \in V}exp(u^T_wv_c)} $$The equation above has some points:
This is an example of the **softmax function: **
$$ softmax(x_i)=\frac{exp(x_i)}{\sum^n_{j=1}exp(x_j)}=p_i $$The softmax function maps arbitrary values $x_i$ : to a probability distribution $p_i$
- “max” because amplifies probability of largest $x_i$ ;
- “soft” because still assigns some probability to smaller $x_i$
variants
Two model variants:
Skip-grams:
Predict context (“outside”) words (position independent) given center word
Continuous Bag of Words (CBOW):
Predict center word from (bag of) context words