NIN

Abstract

本文提出了一种新的网络结构，称为 “网络中的网络”(NIN)，以提高模型对感受野内局部图块的可辨别性。传统的卷积层使用线性滤波器和非线性激活函数来扫描输入。相反，本文建立了结构更复杂的微神经网络，以抽象出感受野内的数据。本文用MLP来实例化微神经网络，MLP是一个有效的函数近似器。通过类似CNN的方式在输入上滑动微网络来提取特征图，然后将它们送入下一层。深度NIN可以通过堆叠多个上述结构来实现。通过微网络加强局部建模，能够在分类层中利用全局平均池化的特征图，这比传统的全连接层更容易解释，也更不容易过拟合。本文在CIFAR-10和CIFAR-100上用NIN取得了最先进的分类性能，其在SVHN和MNIST数据集上也有合理的表现。

1 Introduction

卷积神经网络[1]由交替的卷积层和池化层组成。卷积层采取线性滤波器和底层感受野的内积，然后在输入的每个局部使用非线性激活函数，由此产生的输出称为特征图。

CNN中的卷积滤波器是基础数据块的广义线性模型（GLM），本文认为GLM的抽象程度很低。这里所说的抽象性是指特征对同一概念的变体是不变的[2]。用一个更有力的非线性函数近似器代替GLM可以提高局部模型的抽象能力。当潜在概念的样本是线性可分离的，即概念的变体都在GLM定义的分离平面的一侧时，GLM可以实现良好的抽象程度。因此，传统的CNN隐含了潜在概念是线性可分离的假设。然而，同一概念的数据往往存在于一个非线性流形上，因此捕捉这些概念的表征通常是输入的高度非线性函数。在NIN中，GLM被一个 “微网络 “结构所取代，它是一个通用的非线性函数近似器。在这项工作中，本文选择MLP[3]作为微网络的实例，它是一个通用的函数逼近器并可通过反向传播训练的神经网络。

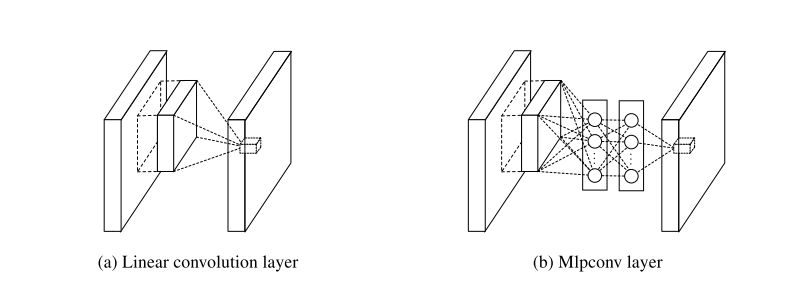
图1：线性卷积层和mlpconv层的比较。线性卷积层包括一个线性滤波器，而mlpconv层包括一个微型网络（本文选择mlp）。这两个层都将局部感受野映射为潜伏概念的置信度值。

由此产生的结构，本文称之为mlpconv层，与图1中的CNN进行比较。线性卷积层和mlpconv层都将局部感受野映射到输出的特征向量上。mlpconv用MLP将输入的局部图块映射到输出特征向量，MLP由多个具有非线性激活函数的全连接层组成，它的权重在所有的局部感受区之间共享。通过在输入上滑动MLP获得特征图，其方式与CNN类似，然后被送入下一层。NIN的整体结构是多个mlpconv层的堆叠。

在CNN中，本文没有采用传统的全连接层进行分类，而是通过全局平均池化层直接输出最后一个mlpconv层的特征图的空间平均值作为类别的置信度，然后将所得向量送入softmax层。在传统的CNN中，由于全连接层作为中间的黑匣子，很难解释来自目标成本层的类别级信息是如何传递回前一个卷积层的。相比之下，全局平均集合更有意义，也更容易解释，因为它强化了特征图和类别之间的对应关系，而这是通过使用微网络进行更强的局部建模实现的。此外，全连接层容易出现过拟合，并严重依赖dropout正则化[4] [5]，而全局平均池化本身就是一个结构正则化器，它天生就能防止整体结构的过拟合。

作者认为传统的GLM在特征提取的过程中根本不能区分这些中间过程里所形成的特征元素，除非这些特征元素是线性可分的。所以，在作者的眼里，传统CNN有效的一个假设就是这些特征元素能够线性可分。

例如在一个用于识别汽车图片的卷积网络模型中，靠前的卷积层会被用于提取一些粗糙的原始的特征（如：线段、棱角等）；而靠后的卷积层则会以前面的为基础提取到更为高级一些的特征（如：轮胎、车门等）。同时，在每个阶段里所形的这些特征原始都被称之为 “latent concept”，因为事实上还有很多抽像的特征我们人类是无法辨认的（它可能是有用的特征，也可能不是），所以被称为“latent”。作者认为，传统的GLM在进行每一阶段的特征提取中，根本不足以区分这些特征元素——例如某个卷积层可能提取得到了很多“轮胎”这一类的same concept，但是GLM区分不了这些非线性的特征（到底是哪一类汽车的轮胎）——所以导致最终的任务精度不那么的尽如人意。

2 Convolutional Neural Networks

经典的卷积神经元网络[1]由交替堆叠的卷积层和空间汇集层组成。卷积层通过线性卷积滤波器再加上非线性激活函数（rectifier, sigmoid, tanh等）生成特征图。以ReLU为例，特征图可以计算如下：

$$ f_{i,j,k}=max(w_k^Tx_{i,j},0). $$

是特征图中每个像素的索引， $x_{ij}$ 表示输入patch$(i, j)$, $k$ 用于索引特征图的通道。

当潜在概念的实例是线性可分离时，这种线性卷积足以实现抽象化。然而，实现良好抽象的表征通常是输入数据的高度非线性函数。在传统的CNN中，这一点可以通过利用一套过度完整的滤波器[6]来弥补，以覆盖潜概念的所有变化。也就是说，可以学习单个线性滤波器来检测同一概念的不同变化。然而，对一个概念有太多的过滤器会给下一层带来额外的负担，它需要考虑上一层的所有变化的组合[7]。如同在CNN中，来自高层的过滤器映射到原始输入中的更大区域。它通过结合下面一层的低级概念来生成一个更高级的概念。因此，本文认为，在将它们组合成更高层次的概念之前，对每个局部图块做一个更好的抽象是有益的。

在最近的maxout网络[8]中，通过对仿生特征图（仿生特征图是不应用激活函数的线性卷积的直接结果）的最大集合来减少特征图的数量。对线性函数的最大化使得一个分片线性逼近器能够逼近任何凸函数。与进行线性分离的传统卷积层相比，maxout网络更有效力，因为它可以分离位于凸集内的概念。这一改进使maxout网络在几个基准数据集上具有最佳性能。

然而，maxout网络强加了一个先验，即潜在概念的实例位于输入空间的凸集内，这并不一定成立。当潜在概念的分布更加复杂时，有必要采用一个更通用的函数近似器。所以本文试图通过引入新颖的 “网中网 “结构来实现这一点，在每个卷积层中引入一个微型网络来计算局部斑块的更抽象的特征。

在以前的一些工作中已经提出在输入上滑动微网络。例如，结构化多层感知器（SMLP）[9]在输入图像的不同斑块上应用共享多层感知器；在另一项工作中，基于神经网络的过滤器被训练用于人脸检测[10]。然而，它们都是为特定的问题而设计的，并且都只包含滑动网络结构中的一个层。NIN是从一个更普遍的角度提出的，微网络被整合到CNN结构中，以寻求对各级特征的更好的抽象。

可以先利用浅层的网络来对各个阶段里所形成的非线性特征元素进行特征表示，然后再通过卷积层来完成分类类别间线性不可分的抽象表示，以此来提高模型最后的任务精度。

3 Network In Network

本文首先强调了提出的 “网中网 “结构的关键部分：MLP卷积层和全局平均池层，分别在第3.1和第3.2节。然后，在第3.3节中详细介绍整个NIN。

3.1 MLP Convolution Layers

鉴于没有关于潜在概念分布的先验，最好使用通用函数近似器对局部斑块进行特征提取，因为它能够对潜在概念的更抽象的表示进行近似。径向基网络和MLP是两个著名的通用函数近似器。本文在这项工作中选择MLP有两个原因。首先，MLP与卷积神经网络的结构兼容，它是用反向传播法训练的。第二，MLP本身可以是一个深度模型，这与特征重用的精神是一致的[2]。这种新型的层在本文中被称为mlpconv，其中MLP取代了GLM对输入进行卷积。图1说明了线性卷积层和mlpconv层的区别。mlpconv层所进行的计算如下所示：

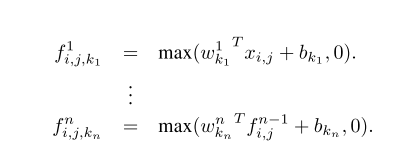
这里$n$是MLP中的层数。MLP中使用ReLU作为激活函数。

从跨通道（跨特征图）池化的角度来看，式2相当于在正常卷积层上的级联跨通道参数池化。每个池化层对输入的特征图进行加权线性重组，然后经过一个ReLU。跨通道池化后的特征图在下一层中再次进行跨通道池化。这种级联式跨渠道参数池结构允许跨渠道信息的复杂和可学习的相互作用。

跨信道参数池层也相当于一个具有1x1卷积核的卷积层，这种解释可以直接理解NIN的结构。

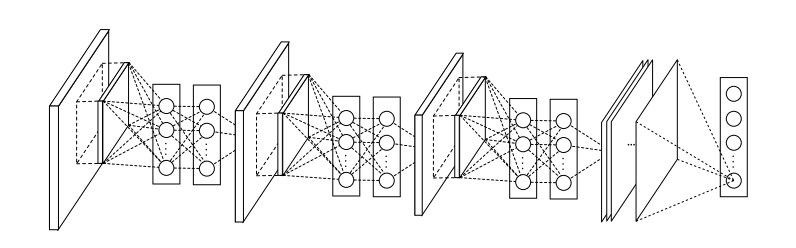
图2：Network In Network的整体结构。在本文中，NINs包括三个mlpconv层和一个全局平均池层的堆叠.

与maxout层的比较：maxout网络中的maxout层在多个仿生特征图上进行max pooling[8]。maxout层的特征图的计算方法如下：

$$ f_{i,j,k}=max(w_{k_m}^{T}x_{i,j}). $$

线性函数的Maxout形成了一个片状线性函数，能够对任何凸函数进行建模。对于一个凸函数，函数值低于特定阈值的样本形成一个凸集。因此，通过近似局部补丁的凸函数，maxout有能力为样本在凸集内的概念形成分离超平面（即$l_2$球、凸锥）。Mlpconv层与maxout层的不同之处在于，凸函数近似器被一个通用函数近似器所取代，它在模拟各种潜在概念的分布方面具有更大的能力。

3.2 Global Average Pooling

传统的卷积神经网络在网络的低层进行卷积。对于分类来说，最后一个卷积层的特征图矢量化，并送入全连接层，然后是softmax逻辑回归层[4] [8] [11]。这种结构是卷积结构与传统神经网络分类器的桥梁。

它将卷积层视为特征提取器，并以传统的方式对产生的特征进行分类。然而，全连接层容易出现过拟合，从而阻碍了整个网络的泛化能力。Hinton等人[5]提出的Dropout是一个正则器，它在训练过程中随机地将全连接层的一半激活值设置为零。它提高了泛化能力，并在很大程度上防止了过拟合[4]。

本文提出了另一种叫做全局平均池的策略，以取代CNN中传统的全连接层。其思路是在最后一个mlpconv层中为分类任务的每个对应类别生成一个特征图。本文不在特征图上添加全连接层，而是取每个特征图的平均值，然后将得到的向量直接送入softmax层。全局平均池比全连接层更好的一个特点是，它通过强制执行特征图和类别之间的对应关系，更符合卷积结构。因此，特征图可以很容易地被解释为类别置信图。另一个优点是，在全局平均集合中没有参数需要优化，因此在这一层可以避免过度拟合。此外，全局平均集合法还总结出了空间信息，因此它对输入的空间平移更为稳健。

可以把全局平均集合看作是一个结构性的正则器，它明确地将特征图强制为概念（类别）的置信图。这是由mlpconv层实现的，因为它们比GLMs更好地接近置信图。

在这篇文章中，作者提出了通过以全局平均池化的方式来代替这部分全连接网络。全局平均池化的具体做法是取最后卷积输出的特征图中每一个特征图的均值来作为其中一个类别的logit值。然后再将其输入到softmax分类层进行分类。因此，这也就意味着如果你需要完成的是一个$k$分类的任务，那么模型最后的卷积输出一定得含有$k$个通道数。

3.3 Network In Network Structure

NIN的整体结构是一个mlpconv层的堆叠，在其之上是全局平均池和目标成本层。像CNN和maxout网络一样，在mlpconv层之间可以添加子采样层。图2显示了一个有三个mlpconv层的NIN。在每个mlpconv层中，都有一个三层感知器。NIN和微网络的层数都很灵活，可以针对具体任务进行调整。

4 Experiments

4.1 Overview

本文在四个基准数据集上评估NIN。CIFAR-10[12]、CIFAR-100[12]、SVHN[13]和MNIST[1]。在这些数据集上测试的网络均由三个堆叠的mlpconv层组成，所有实验中的mlpconv层后面都有一个空间最大集合层，该层对输入图像进行了2倍的降样。作为一个正则器，除最后一个mlpconv层外，所有的输出都被应用了dropout。除非特别说明，在实验部分使用的所有网络都使用了全局平均池，而不是在网络的顶部使用全连接层。另一个应用的正则方法是Krizhevsky等人[4]使用的权重衰减。图2说明了本节中使用的NIN网络的整体结构。本文在Alex Krizhevsky[4]开发的超快速cuda-convnet代码基础上实现本文网络。数据集的预处理、训练集和验证集的分割都是按照Goodfellow等人[8]的做法。

本文采用Krizhevsky等人[4]使用的训练程序。网络训练的mini-batch为128。训练过程从初始权重和学习率开始，一直持续到训练集上的准确度不再提高，然后学习率按10的比例降低。这个过程重复一次，使最终的学习率为初始值的百分之一。

4.2 CIFAR-10

CIFAR-10数据集[12]由10类自然图像组成，共有50,000张训练图像，以及10,000张测试图像。每张图像都是大小为32x32的RGB图像。对于这个数据集，本文采用与Goodfellow等人在maxout网络[8]中使用的相同的全局对比度归一化和ZCA白化。使用训练集的最后10,000张图像作为验证数据。

在这个实验中，每个mlpconv层的特征图的数量被设置为与相应的maxout网络中的数量相同。使用验证集调整两个超参数，即局部感受野的大小和权重的衰减。之后，超参数被固定，用训练集和验证集从头开始训练网络。得到的模型被用于测试。本文在这个数据集上得到了10.41%的测试误差，与最先进的方法相比，这个误差提高了1%以上。与以往方法的比较见表1。

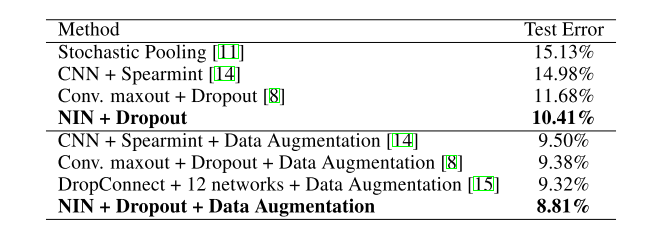
表1：各种方法对CIFAR-10的测试集错误率。

在本文的实验中发现，在NIN中的mlpconv层之间使用dropout可以通过提高模型的泛化能力来提升网络的性能。如图3所示，在mlpconv层之间引入dropout层后，测试误差减少了20%以上。这一观察结果与Goodfellow等人[8]一致。因此，本文中使用的所有模型都在mlpconv层之间加入了dropout。在CIFAR-10数据集上，没有dropout正则器的模型实现了14.51%的错误率，这已经超过了许多以前带有正则器的先进技术（maxout除外）。由于不含dropout的maxout的性能不可用，本文只对dropout的正则化版本进行了比较。

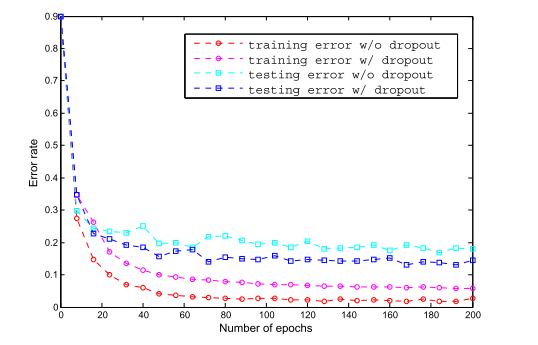
图3：mlpconv层之间的dropout的正则化效果。图中显示了在训练的前200个 epochs中，有和没有dropout的NIN的训练和测试误差。

4.3 CIFAR-100

CIFAR-100数据集[12]的大小和格式与CIFAR-10数据集相同，但它包含100个类别。因此，每个类中的图像数量只有CIFAR-10数据集的十分之一。对于CIFAR-100，不调整超参数，而是使用与CIFAR-10数据集相同的设置。唯一的区别是，最后一个mlpconv层输出100个特征图。CIFAR-100的测试误差为35.68%，超过了目前没有数据增量的最佳性能1%以上。性能比较的细节显示在表2中。

表2：各种方法对CIFAR-100的测试集错误率。

4.4 Street View House Numbers

SVHN数据集[13]由630,420张32x32的彩色图像组成，分为训练集、测试集和一个额外集。这个数据集的任务是对位于每个图像中心的数字进行分类。训练和测试程序遵循Goodfellow等人[8]。即从训练集中每类选择400个样本，从额外集中每类选择200个样本，用于验证。训练集和额外集的其余部分被用于训练。验证集仅作为超参数选择的指导，但从未用于训练模型。

数据集的预处理再次遵循Goodfellow等人[8]的做法，即局部对比度归一化。SVHN中使用的结构和参数与CIFAR-10中使用的结构和参数相似，由三个mlpconv层组成，然后是全局平均池。对于这个数据集，本文得到的测试错误率为2.35%。将结果与没有增强数据的方法进行比较，比较结果见表3。

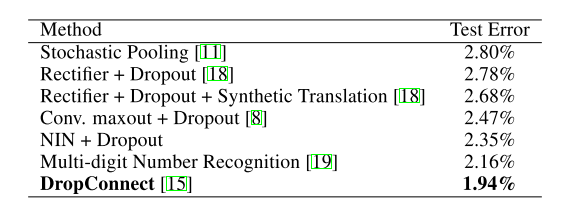
表3：各种方法的SVHN的测试集错误率。

4.5 MNIST

MNIST[1]数据集由手写数字0-9组成，尺寸为28x28。总共有60,000张训练图像和10,000张测试图像。对于这个数据集，我们采用了与CIFAR-10相同的网络结构。但从每个mlpconv层产生的特征图的数量减少了。因为MNIST与CIFAR-10相比是一个更简单的数据集；需要的参数更少。本文在这个数据集上进行了测试，而没有进行数据增量。其结果与以前采用卷积结构的工作进行了比较，见表4。

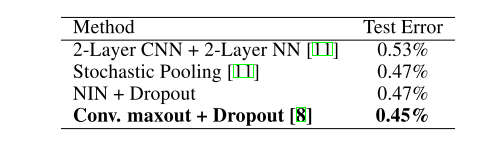
表4：各种方法对MNIST的测试集错误率。

由于MNIST已经被调整到非常低的错误率，取得了与目前最好的成绩（0.47%）相当但不更好的成绩。

4.6 Global Average Pooling as a Regularizer

全局平均池，转换矩阵是有前缀的，它只在共享相同数值的块对角线元素上是非零的。全连接层可以有密集的转换矩阵，其值要经过反向传播的优化。为了研究全局平均池化的正则化效应，本文用全连接层取代全局平均池化层，而模型的其他部分保持不变。对这个模型进行了评估，在全连接线性层之前有和没有丢弃。两种模型都在CIFAR-10数据集上进行了测试，其性能比较见表5。

表5：与全连接层相比，全局平均池化。

如表5所示，没有dropout正则化的全连接层的性能最差（11.59%）。这是预料之中的，因为如果不应用正则化，全连接层就会过度适应训练数据。在全连接层之前添加dropout可以减少测试误差（10.88%）。全局平均池在三者中取得了最低的测试误差（10.41%）。

然后探讨全局平均池对传统CNN是否有同样的正则化效果。 本文实例化了Hinton等人[5]所描述的传统CNN，它由三个卷积层和一个局部连接层组成。局部连接层产生16个特征图，这些特征图被馈送到一个有dropout的全连接层。为了使比较公平，本文将局部连接层的特征图数量从16个减少到10个，因为在全局平均池化方案中，每个类别只允许有一个特征图。然后，通过用全局平均池化方案替换掉dropout+全连接层来创建一个全局平均池化的等效网络。在CIFAR-10数据集上测试了这些性能。

这个全连接层的CNN模型只能达到17.56%的错误率。当加入dropout时，本文取得了与Hinton等人[5]报告的类似的性能（15.99%）。在这个模型中，通过用全局平均池代替全连接层，得到了16.46%的错误率，与没有dropout的CNN相比，有1%的提高。这再次验证了全局平均池化层作为正则器的有效性。虽然它比dropout正则器的结果略差，但本文呢认为全局平均池化对线性卷积层的要求可能太高，因为它需要带有整流激活的线性滤波器来模拟类别的置信图。

5 Conclusions

本文为分类任务提出了一种新的深度网络，称为 “网络中的网络”（NIN）。这种新的结构由mlpconv层和全局平均池层组成，前者使用MLP对输入进行卷积，后者替代了传统CNN中的全连接层。mlpconv层对局部斑块进行了更好的建模，而全局平均池则作为一种结构上的正则器，防止全局的过度拟合。利用NIN的这两个组成部分，本文在CIFAR-10、CIFAR-100和SVHN数据集上展示了最先进的性能。通过对特征图的可视化，证明了来自NIN的最后一个mlpconv层的特征图是类别的信心图。