Leetcode-75 总结

代码链接：KurongTohsaka/my-lc75-go

Array&String

151 反转字符串中的单词：双指针。
238 除自身以外数组的乘积：线性 DP 。
334 递增的三元子序列：双指针。
345 反转字符串中的元音字母：双指针。
443 压缩字符串：双指针。
605 种花问题：列出三种种花情况，依次进行处理即可。
1071 字符串的最大公因式：根据特殊的 str1 + str2 == str2 + str1 公式和辗转相除法解题。
1431 拥有最多糖果的孩子：先找最大值，然后进行比较。
1768 交替合并字符串：取较小长度最为切割位置，然后交替合并，最后处理剩余部分。

DoublePointers

11 接水问题：双指针的首尾指针。
283 移动零：双指针的快慢指针。
392 判断子序列：双指针的快慢指针。
1679 K 和数对的最大数目：解法与两数之和相似，使用哈希表记录为匹配数组次数，然后更新 hashMap[k-v] 的数值。

SlidingWindow

643 子数组最大平均数-1 ：定长滑动窗口，应用通用解法，即新元素进入、更新统计量、right-left+1 元素离开三步。
1004 最大连续1的个数-2 ：变长滑动窗口，通过快慢指针实现。
1456 定长子串中元音的最大数目：定长滑动窗口，通用解法。
1493 删掉一个元素后全为1的最长子数组：变长滑动窗口，解法与 1004 高度相似。

PrefixSum

724 寻找数组的中心下标：双指针可解，不过还是推导出的公式更快。
1732 找到最高海拔：很简单，直接秒。

HashMap

1207 独一无二的出现次数：用了两个哈希，第一个是对数组中所有元素进行计数，第二个是对第一个哈希元素的出现次数进行计数，目的是得到独一无二的出现次数。
1657 确定两个字符串是否接近：操作 1 和 2 能实现的大前提是两个字符串的长度一致，操作 1 只要两个字符串对应的字母的计数一致就成立，操作 2 则进一步要求每个“次数”一致。
2215 找出两数组的不同：双哈希表记录每个元素出现次数，然后分别进行比较。
2352 相等行列对：一个哈希表解决。先行遍历，把每一行作为键存储，然后记录相同的行出现的次数。再列遍历，把每列作为键去查询，然后把次数加上相同的行的个数。

Stack

394 字符串解码：
- 本题要点在于只要遇到右括号就开始处理栈内元素：
  - 先处理直到左括号内的所有元素，拼接后再反转（顺序是反的🐎），然后别忘记让左括号出栈。
  - 之后统计出现次数，此时注意数字可能为两位数。在处理完成后，就开始按照次数重复拼接子串，然后再把该子串入栈（处理嵌套字符串的方式）。
735 小行星碰撞：只有当栈顶向右（正）且当前行星向左（负）时才处理碰撞，使用循环处理可能的多次碰撞，直到当前行星被摧毁或无法继续碰撞。
2390 从字符串中移除星号：常规栈解法，很简单。

Queue

649 Dota2 参议院：使用两个队列存储每位参议院出现的位置，通过比较位序来选择被淘汰的议员，同时保证每轮必有两名议员被踢出队列。
933 最近的请求次数：维护一个队列，本题想要的结果就是最终的队列长度。超出时间范围的请求出队、新请求进队。

LinkedList

206 反转链表：经典操作，三指针反转链表，属于基本功了。
328 奇偶链表：用两个变量记录奇偶两个链表的头节点，再用两个变量作为构建奇偶链表的指针。然后遍历整个链表去构建奇偶链表，最后把奇链表的指针指向偶链表的头部。
2095 删除链表中的中间节点：通过快慢指针找到中间节点，同时记录慢指针的前一个节点方便后续删除操作。
2130 链表最大孪生和：本题属于缝合题，先是快慢指针找中间节点，再是反转后半部分链表，最后又是一个双指针遍历。

Tree - DFS

所有题都是。DFS （深度优先遍历）。

104 二叉树的最大深度：自底向上进行递归，遍历到叶节点时返回深度。不断维持左右子树的最大深度并返回。
236 二叉树的最近公共祖先：参见代码注释。
437 路径总和 3：这道题是前缀和+回溯的形式。在二叉树上，前缀和相当于从根节点开始的路径元素和。用哈希表 cnt 统计前缀和的出现次数，当我们递归到节点 root 时，设从根到 root 的路径元素和为 sum，那么就找到了 cnt[sum−targetSum] 个符合要求的路径，加入答案。
872 叶子相似的树：先单独找到每棵树的叶序列，再进行对比。
1372 二叉树中的最长交错路径：zigzag 锯齿状路径，必须满足每个相邻节点的“方向”不同。所以在处理递归时，需要额外维护 direction 前进方向。进入下一个递归时，方向必须保持与当前遍历方向不同，如果相同，就以当前节点为新起点进行下一次递归。
1448 统计二叉树中好节点的数目：递归返回的值为计数，关键在于把左右子树的递归遍历放在何处，这里是让计数直接与左右子树的结果相加。

Tree - BFS

199 二叉树的右视图：处理当前层节点时，先右子节点后左子节点入队，保证下层队列按右到左排列，使得下次循环队首即最右节点。此时，将当前层第一个节点的值加入结果（即最右节点）。
1161 最大层元素和：标准的层序遍历。注意维护最大和、最小层两个变量即可。

BinarySearchTree

450 删除二叉搜索树中的节点：比较复杂，需要考虑进行节点删除的两种情况。一种是删除节点为叶节点或单侧为空，另一种是删除节点的两侧非空。前者直接进行节点的替换即可，后者需先找到某侧的最大值节点作为继任者，然后删除当前节点，最后完成节点的替换。
700 二叉搜索树中的搜索：标准的迭代过程。

Graph - DFS

399 除法求值：本题先建立每个变量对应的邻接表索引，然后初始化邻接表、用计算结果构建邻接表。然后是本题的核心点，用 Floyd 算法计算所有可能的访问路径。最后处理所有的查询。
547 省份数量：图的深度优先遍历，以访问数组为入口进行遍历。进入遍历函数后，根据每个节点的数组继续递归。
841 钥匙和房间：图的深度优先遍历。必须要维护一个访问数组，记录节点访问情况。这里的深度优先遍历的参数是图本身和要访问的节点。当一个节点记录完成，就把相应节点中存在的值依次输入到递归函数中。
1466 重新规划路线：题目可以转化为“从城市 0 出发，所有道路的方向必须指向 0 或其子节点”。因此需要统计所有“背离 0”的道路数量。
- 将所有路径保存到邻接表中，然后开始 DFS：
  - 从城市 0 出发，沿着所有可能的道路遍历。
  - 如果遇到原始方向的道路（edge[1] == 1），说明这条道路的方向是背离 0 的，需要反转。
  - 递归累加所有需要反转的道路数量。

Graph - BFS

994 腐烂的橘子：本题是 BFS 的升级版多源 BFS，可以看到一开始需要确定所有 BFS 开始的源点。后面的 BFS 模版略有变化，需要额外加一层遍历多源点的循环。
1926 迷宫中离入口最近的出口：BFS 按层遍历，第一次到达出口时的步数一定是最小的。图的 BFS 过程与之前写的树的 BFS 相似，通过队列存储访问节点，然后循环以队列长度为条件。

Heap&PriorityQueue

215 数组中的第 K 个最大元素：标准最大堆实现。
2336 无限集中的最小数字：标准最小堆实现。
2462 雇佣 K 位工人的总代价：两个最小堆+双指针，最小堆使用标准库实现。
2542 最大子序列的分数：放弃。

BinarySearch

182 寻找峰值：只需要比较 nums[mid] 和 nums[mid+1] 就能确定峰值的可能方向。利用二分查找的思想，通过比较局部信息来缩小搜索范围，无需有序数组。这是二分查找的一种变体，适用于具有特定单调性或局部极值的问题。
374 猜数字大小：这道题的表述有大问题，其实就是调用 guess 函数（本题提供）看返回的结果如何。然后用二分查找，通过区间中的中间值来不断更新上下界。
875 爱吃香蕉的珂珂：本题存在某种单调性，适合用二分查找。这里的二分查找的范围注意不是索引范围，而是吃香蕉的速度，所以最小为 1 。
2300 咒语和药水的成功对数：通过 (int(success)-1)/spell+1 计算得到二分查找的目标值。

Backtrace

17 电话号码的字母组合：回溯解法，这里的回溯是 DFS 写法。
216 组合总和3：回溯解法，还是 DFS 写法。这里需要注意当递归终止条件触发时，加入的应该是 combination 的复制（因为该变量还需要变更）。每次递归都要从 start 开始依次遍历，这里有一个剪枝条件 sum+i > n 。

DynamicProgramming - 1D

198 打家劫舍：状态转移方程 cache[i] = max(cache[i-1], cache[i-2]+nums[i-1]) ，cache[i] 表示到第i个房屋为止所能偷取的最大金额，cache[i-1] 表示相邻房屋的最大值，不加 nums[i-1] 因为相邻房屋不能连续偷取。
746 使用最小花费爬楼梯：本题是 0-1 背包的变形，0-1 对应的两个选择是登一级或登两级阶梯。楼梯为 0~n-1 级，楼梯顶对应 n 级。设 cache[n] 表示直到第 n 级阶梯的最小花费，costs[n] 表示从第 n 级阶梯向上爬花费。则 cache[0], cache[1] 用于初始化，从 cache[2] 开始计算：cache[n]=min{cache[n-1]+costs[n-1], cache[n-2]+costs[n-2]}
790 多米诺和托米诺平铺：设 f[i] 表示平铺 2*i 面板的方案数，f[n] 即为所求。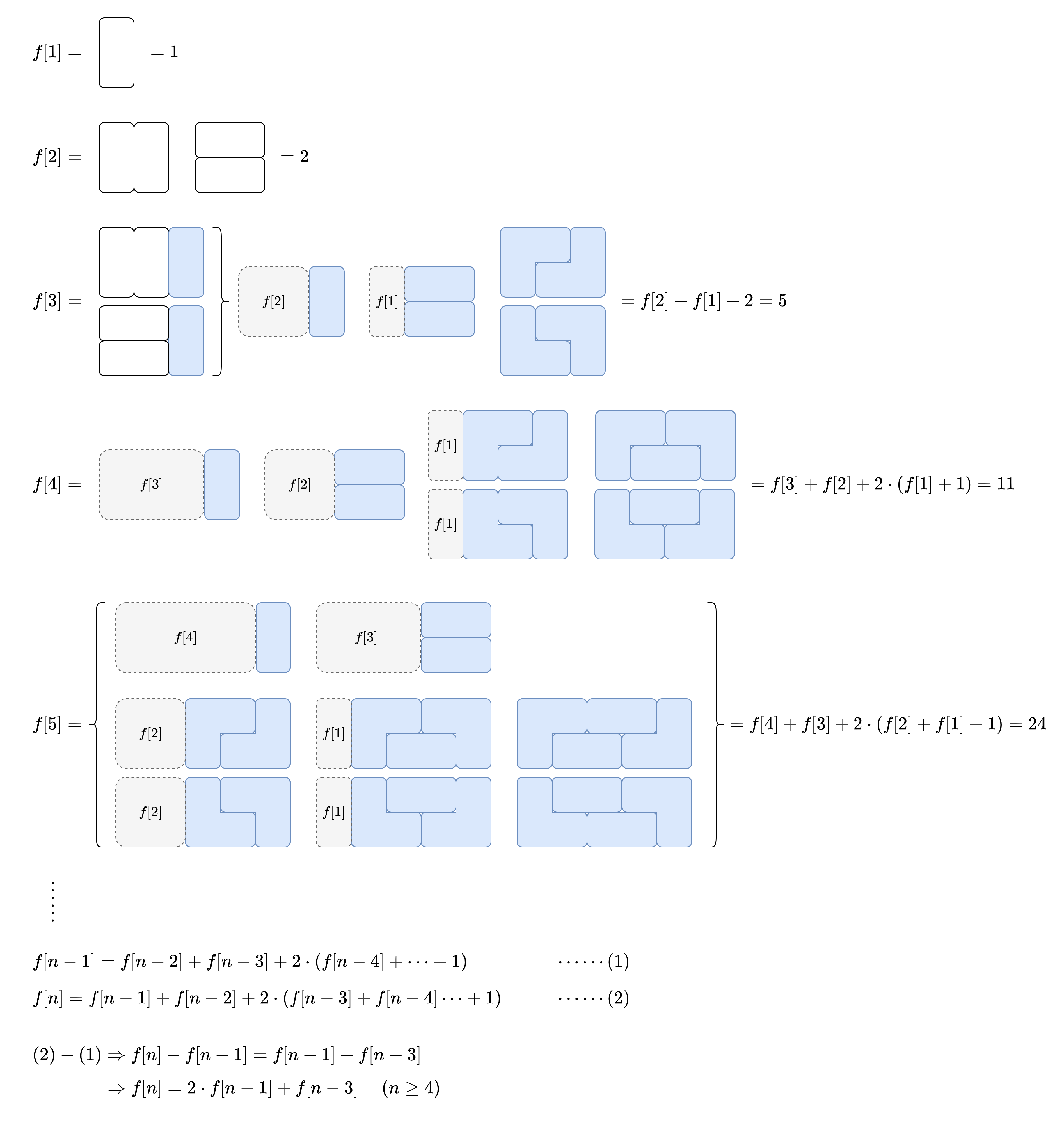
- 先找到上图中的规律，然后将递推式与 1e9 + 7 取模运算得到答案。
1137 第N个泰波那契数：前缀和，动态规划的前置步骤。

DynamicProgramming - MultiD

62 不同路径：状态转移方程分为三种，一个是在第一行只能向右走，一个是在第一列只能向下走，另一个则是向右向下都可以。分别对应的状态转移方程如下：$cache[i][j] = cache[i][j-1]$ 、 $cache[i][j] = cache[i-1][j]$ 、 $cache[i][j] = cache[i-1][j] + cache[i][j-1]$ .
72 编辑距离：经典难度是 Hard ，结果内卷成 Medium 了。我们使用一个二维数组 dp（代码中的 cache），其中 dp[i][j] 表示将 word1 的前 i 个字符转换为 word2 的前 j 个字符所需的最少操作次数。
- 初始化：
  - dp[0][j]：将空字符串转换为 word2 的前 j 个字符，需要进行 j 次插入操作。
  - dp[i][0]：将 word1 的前 i 个字符转换为空字符串，需要进行 i 次删除操作。
- 对于 dp[i][j]，我们需要考虑 word1[i-1] 和 word2[j-1]（因为字符串索引从 0 开始）：
  1. 如果 word1[i-1] == word2[j-1] ：
    - 当前字符相同，不需要操作，直接继承 dp[i-1][j-1]。
    - dp[i][j] = dp[i-1][j-1]
  2. 如果 word1[i-1] != word2[j-1] ：
    - 需要进行插入、删除或替换操作：
      - 插入：在 word1 的第 i 个位置插入 word2[j-1]，此时 word1 的前 i 个字符与 word2 的前 j-1 个字符匹配。操作数为 dp[i][j-1] + 1。
      - 删除：删除 word1 的第 i 个字符，此时 word1 的前 i-1 个字符与 word2 的前 j 个字符匹配。操作数为 dp[i-1][j] + 1。
      - 替换：将 word1[i-1] 替换为 word2[j-1]，此时 word1 的前 i-1 个字符与 word2 的前 j-1 个字符匹配。操作数为 dp[i-1][j-1] + 1。
    - 取这三种操作的最小值：
      - dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
714 买卖股票的最佳时机：设 cache[i][0] 为第 i 天结束时不持有股票的最大利润，cache[i][1] 为第 i 天结束时持有股票的最大利润。第 i 天不持有股票时，由两种状态转移而来，即前一天也不持有股票，前一天持有股票今天卖出。第 i 天持有股票时，由两种状态转移而来，即前一天也持有股票，前一天不持有股票今天买入。关于 fee 的计算，一次完整交易包含一次买入、一次卖出，所以只需要减一次。
1143 最长公共子序列：经典的二维DP题。状态转移方程分为两种情况，当前字符相等时 $cache[i][j] = cache[i-1][j-1] + 1$ ，不等时 $cache[i][j] = max(cache[i-1][j], cache[i][j-1])$ 。这两个方程还是比较好想的，相等时就是 cache[i-1][j-1] 再增加一个公共字符，不等时就是 cache[i-1][j] 和 cache[i][j-1] 选一个最大的。

Bitwise

136 只出现过一次的数字：用到了异或运算的结合律，即 $(a⊕b)⊕c=a⊕(b⊕c)$（类比加法）。
338 比特位计数：x &= x - 1 这一步作用是去掉最低位的 1 ，直到把所有 1 都去掉。
1318 或运算的最小翻转次数：逐位进行操作，注释有详细解释。

Trie

208 实现前缀树：手搓前缀树，面试很少考，原理可以看看。
1268 搜索推荐系统：手搓前缀树解法。

IntervalSet

435 无重叠区间：贪心解法，将问题改为计算最多可以选多少个互不重叠的区间，那么没选的区间就是要移除的区间。先对区间进行排序，优先选择结束早的区间，可以留下更多空间给后续区间，从而最大化不重叠区间的数量。
452 用最少数量的箭引爆气球：该题解法也是贪心，属于贪心区间问题。贪心算法在区间问题中的核心思想是通过某种排序和局部最优选择，达到全局最优解。
- 排序：通常按区间起点或终点排序。例如：按右端点排序（如本题）：方便选择箭的位置。按左端点排序：适用于合并区间等问题。排序的目的是让区间有序，便于贪心策略的局部最优选择。
- 贪心策略：初始化关键变量（如 pre 表示前一个选择的点）。遍历排序后的区间，根据题目要求选择是否更新关键变量：如果当前区间与已选区间无重叠（或满足题目条件），则更新关键变量并增加计数。否则，跳过或合并区间。

MonotonicStack

739 每日温度：用的单调栈，这里用的是单调递减栈。通过单调栈的特性，存储待处理的索引（温度逐渐降低）。然后碰到温度升高时，依次处理栈中元素。
901 股票价格跨度：题目的意思是找上一个大于它的元素的位置，那么就必须存储连续个比它小的元素才能计算跨度。本题也是单调栈的经典应用，本题是单调递减栈。

Leetcode-75 总结#

Array&String#

DoublePointers#

SlidingWindow#

PrefixSum#

HashMap#

Stack#

Queue#

LinkedList#

Tree - DFS#

Tree - BFS#

BinarySearchTree#

Graph - DFS#

Graph - BFS#

Heap&PriorityQueue#

BinarySearch#

Backtrace#

DynamicProgramming - 1D#

DynamicProgramming - MultiD#

Bitwise#

Trie#

IntervalSet#

MonotonicStack#

Leetcode-75 总结

Array&String

DoublePointers

SlidingWindow

PrefixSum

HashMap

Stack

Queue

LinkedList

Tree - DFS

Tree - BFS

BinarySearchTree

Graph - DFS

Graph - BFS

Heap&PriorityQueue

BinarySearch

Backtrace

DynamicProgramming - 1D

DynamicProgramming - MultiD

Bitwise

Trie

IntervalSet

MonotonicStack